タグ:中学校

6月15日、板橋区立板橋第一中学校の2学年の社会科で、「教科書を読み解きながら期末テストに備える」授業をしました。

その１では、教科書見開き2ページからの検索課題の指導法をご紹介しました。中学生でも教科書の「使い方」が身に着いていない生徒が少なくないことを実感していただけたのではないかと思います。その２では第二次・第三次産業の定義、及び教科書の資料部分を活用して、身近な企業を第二次・第三次産業に根拠をもって分類する具体例同定の指導法を取り上げました。今回は、RSTでいうところの「イメージ同定」の力を測る問３についてご紹介します。

RSTや「読み解く力」では、説明文に掲載されている非テキスト情報を「イメージ」と呼びます。グラフ・表や図、説明的なイラスト、年表、数式、譜面などがイメージに含まれます。テキスト情報とイメージと正しく結びつける力を「イメージ同定」と呼んでいます。

問３．他の工業地帯と比べたとき、中京工業地帯の特徴（とくちょう）を3つ文章で挙げなさい。

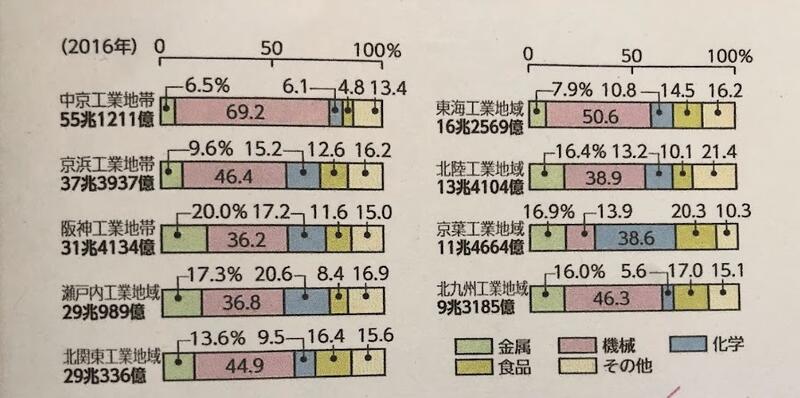
教科書の本文には、一般的な第二次産業の特徴については書かれていますが、中京工業地帯については書かれていません。（中京工業地帯の詳しい特徴は、実は小学校5年生で習います。こちらの授業の前後に学びます。）この問題は本文ではなく、教科書に掲載されている資料３「日本の工業地帯・工業地域と出荷額の割合」の帯グラフ、円グラフ、地図を読み解いて答えなければなりません。特に次の図が重要になります。

（教育出版「中学社会　地理　地域に学ぶ」169ページ、「日本の工業地帯・工業地域と出荷額の割合」より）

教科書の該当箇所で「中京工業地帯」の文字が出てくるのは、資料３だけなので、まず「検索」の力でこの図にたどり着けるか、が最初の関門になります。本文ばかり見ている生徒には「見開き2ページで『中京工業地帯』というキーワードが出てくるのはどこか、探してごらん」を促します。資料３に目が行ってしばらくしても手が動かないときは、「帯グラフのどれが中京工業地帯かな？」と尋ね、中京工業地帯の帯グラフに注目できているか確認します。

その上で、尋ねます。「ぱっ、と見て、中京工業地帯の特徴で気づくことはない？」と。

すると、多くの子は「ピンクが多い」と答えます。

「ピンクってなんだろう？」と尋ねると、「わからない」という答えが多く聞かれました。

グラフの右下に、緑は金属（工業）、ピンクは機械（工業）と読み方が書いてあるのですが、そこに至れない生徒が少なくないのです。ひとりも取り残さない教育を目指すなら、グラフの読み方を、教科書を使って、繰り返し指導する必要があることがわかります。

「ここに色分けの意味が書いてあるよ」と指すと、「あ。」とつぶやき、文章を書き始めることができました。

さて、答え合わせです。

「機械が多い」

これを書いた生徒が多数いました。しかし、これでは、「中京工業地帯には機械が多い」のか「中京工業地帯には機械工業の会社が多い」のか「機械工業の生産量が多い」のか「機械工業に従事する人の数が多い」のか、わかりません。では、わかるようにするにはどうしたらよいか。

そこで、小学5年生のときに習った（はずの）帯グラフの読み方をとり出して指導しました。

１．グラフのタイトルは何か。単位は何か。

２．全体を見て、わりあいがいちばん多いのはどれか。

３．増えているもの、減っているもの、変化がはげしいものはどれか。

４．全体の数字はどのように変化しているか。

５．共通していえることはないか。

６．全体のけいこうから、これからの変化を予想できるか。

（東京書籍　新編「新しい社会５下」6ページより）

 

 

帯グラフには、複数のものを比較する場合と、経年変化を見る場合があります。３，４，５，６は後者のための「読み方」で、１，２が今回必要になる帯グラフの読み解き方です。

資料のタイトルは「日本の工業地帯・工業地域と出荷額の割合」です。ですから、多いのは「出荷額」でしょう。（残念ながら、教育出版のこのグラフには「単位」が書いてありません。改善を期待します。）ピンク（機械）が多い、ことを表現するには、グラフのタイトルから「出荷額（にしめる）」「割合」という言葉をもってきて、先ほどの答えを補います。

「出荷額にしめる機械工業の割合が大きい。」

このように書ければ正解です。「出荷額にしめる機械工業の割合が、5割に近い。」などもよいでしょう。

多い方に注目したら次は、少ないものにも注目します。すると、ブルー（化学）や黄色（食品）が少ないことに気づきます。もう「ブルーが少ない」と書く生徒はいません。

「出荷額にしめる化学工業の割合が小さい。」

「出荷額にしめる食品工業の割合が小さい。」

などを挙げることができました。全体をながめたときに気づくのが、中京工業地帯の出荷額全体の多さです。

「日本で一番出荷額が多い工業地帯である。」

「どの工業地帯・工業地域より出荷額が多い。」

のように自発的に書ける生徒が多くいました。

ところで、資料３の地図と本文にひっぱられたのか「太平洋ベルトにある」と書いた生徒がいました。これは不正解です。なぜなら「他の工業地帯と比べたとき、中京工業地帯の特徴を挙げなさい」と問われているので、他の工業地帯と「異なる点」を挙げなければいけないからです。他の工業地帯の多くも太平洋ベルトにあります。

これで問１～問３まで答え合わせができました。最後に私は次のように語りかけました。

「問３はテストで配点が高い問題です。問３をスラスラ書けたら日比谷高校も夢ではありません。さて、問３は『頭が良くて、才能がないと』解けない問題だったでしょうか？いいえ、違います。『ピンクが多い』『ブルーが少ない』ということがわかり、グラフの読み方を覚えれば誰もが書くことができますね。誰もができるはずのことをきちとできれば日比谷高校に合格できる、ということです。」

ここで「よっし！」とこぶしを突き上げる元気な生徒が数名いました。

「ただし、『機械が多い』と『出荷額にしめる機械工業の割合が大きい』と書けるかどうか、その差が今の君たちと日比谷高校に入学した生徒の違いでしょう。」

すると、「あー、やっぱりだめか・・・」という落胆する声が聞こえます。

「大丈夫です。なぜなら、高校入試は明日ではなく1年半後にあるからです。今日から、基本の教科書の読み方、グラフや表の読み方をしっかり身に着けて学習すれば、きっと望む学校に入学することができるでしょう。」

もう一度「よっし！」と元気に言ってくれてよかったです。

今回の授業で、私はひとつも「社会科のコンテンツを教える」ということはしていません。面白い話もしていません。ただ、教科書の読み方、グラフの読み方のコツを伝授しただけです。

中学校は義務教育の総仕上げの時期です。先生方には、コンテンツを教え込むことから、じょじょに生徒の自学自習に伴走する学習支援者を目指してほしいと思います。そして、すべての子が「自学自習するスキル」を身に着けて卒業してほしいと願っています。自学自習のベースは、「説明文を読み解く力」と「説明文を書く力」です。それらは、特別な才能がなくても、適切な指導と学ぶ機会があれば（自動車の運転免許を得るのと同じように）身に着くはずの力です。そして、「学校」は、まさに、そのようなスキルを着実に身に着ける場所として、社会に存在しているのではないでしょうか。

 

 

まだ最高気温が30度になる沖縄で、研究授業を実施しました。

今回、お招きいただいたのは沖縄県立球陽中学校です。中高一貫の公立学校です。迎えてくれたのは中学3年生の生徒のみなさん。礼儀正しく明るい笑顔が印象的な学校です。

授業のテーマは「偽定理を探せ！」

これは中学1年生から大学生までどの学年でも実践していただける授業として、『AIに負けない子どもを育てる』（新井紀子著、東洋経済新報社、2019年）でも紹介しています。冒頭で、「真偽が決まる文を命題という」という定義を紹介し、どのような文が命題で、どのようなものはそうでないかを区別できるようにします。その上で、真であることが証明された命題を「定理」と呼ぶと説明し、「今日、皆さんは数学者になって、命題の真偽を見分け、真だと思うものには証明をつけましょう。偽だと思うものには、偽である証拠を見つけましょう」と活動の概要を説明しました。

ここまで約5分ですが、すでに球陽中が、私が今まで「偽定理を探せ！」を指導した中で、ずば抜けて「よく耕されたクラス」であることを感じました。

よく耕されたクラスの特徴は、「集中できる」「聞ける」「待てる」にまず現れます。「どれが定理かどうかなんて、自分には関係ない」と思えば急速に興味を失うものです。経験が限られている児童生徒は、どうしても視野が狭い面があります。「待てない」「聞けない」ことで、可能性を狭め、世界への窓を閉じてしまうのを見ると残念に思います。

このクラスは、5分間、一人も脱落せずに話を聞いているので、今日はだいぶ先に連れて行ってあげられるな、と直感しました。

 最初の問題は定番の「0は偶数か」問題です。

0は偶数である。

 偶数に手を挙げた生徒が圧倒的多数でした。（※RSTで大学生や一般社会人の3人に2にが「０は偶数ではない」を選ぶのに比べて、球陽中の3年生がいかに定義を正確に読めるか、がわかります。）ただ、数名「これは偽定理」だと言いました。

意見が割れたときには、定義に戻ることが重要です。

偶数の定義は？というと手を挙げて次のように答えてくれた生徒がいました。

２で割り切れる整数を偶数という。

「0　割る」と聞くと、「できない」と反応するRST受検者は少なくありません。「どんな数も0では割れない」ということと混同しているのでしょう。0は２で割り切れます。やってみましょう。

0÷２＝0　あまり　０

つまり、これは真の命題で、しかも証明がつきましたから、「定理」になりました。

ここで、「偶数を他の文章で定義できますか？」と聞きました。すると、

「整数の並びは偶数、奇数、偶数、奇数、・・・と順番に繰り返す」という意見が出ました。

「でも、整数の並びは、奇数、偶数、奇数、偶数、・・・と順番に繰り返しているともいえるのではありませんか？」と問いかけると、はっとして、「ああ、確かにそうです。これではだめです」と返事がありました。このように指摘をされたときに、自分で「はっ」とする、ことが学びではとても重要です。はっとして、ああそれではだめだと思うから自分で修正ができるのですから。「はっ」とする瞬間、子どもは一番自分ごととして学ぶと感じます。

そうこうしているうちに「２の倍数を偶数といいます」という意見が出ました。私が「変数を使ってみませんか？」と誘うと、「$$2n$$で表される整数。（ただし、$$n$$は整数）」という意見も出ました。定義は何種類か持っていると使い勝手が良いのです。それはおいおいわかってきます。

次も定番問題です。

どんな素数も奇数である。

まず、素数の定義から振り返りました。

１とそれ自身以外は約数をもたない、１より大きい整数を素数という。

素数の定義は数学でしかありえないような複雑な形をしています。悪文といってもいいでしょう。けれども、それ以外表現のしようがないのです。平易な文では表現できないことが科学の中にはたくさんあります。

球陽中ではあっという間に、これは「偽定理」だと見抜かれました。理由は「２は偶数で素数だから」です。「反例」です。反例をみつければ、偽定理だということを簡単に説得できます。

次に挑んだのは次の命題です。

連続する２つの整数の和は、奇数になる。

こういうシンプルな命題を証明するにはコツがあります。それは式にすることです。式の中には「ことば」を含めることはできません。「連続する２つの整数の和」を式にするにはどうしたらよいだろう。

そう、変数を使えばいいんです。

連続する２つの整数の和は、$$n$$を整数として、$$n+(n+1)$$と表すことができる。 $$n+(n+1)=2n+1$$ なので、これは奇数である。

式にすることの良さは「式にすれば勝手に式が考えてくれるところ」（by ライプニッツ）にあります。変形すると、「奇数だ」という証拠が出てくるわけです。先ほど、偶数の定義として、「$$2n$$（ただし$$n$$は整数）と表せる数」という確認をしておいたことが、ここで効いてきます。

このクラスならば大丈夫と思い、最後はちょっと難しい問題を出しました。

連続する２つの整数の積は偶数になる。

一般に、いくつかの数に、ひとつでも偶数が混じっていれば、その積は偶数になります。

多くの生徒が「$$n(n+1)=n^2+n$$」という式を前に「うーん」と悩んでいます。その悩める時間の長さこそが、生徒の伸びしろになります。

ここには答えは書きません。みなさんもぜひ「うーん」と悩んでみてください。

10月1日、令和2年度板橋区学びのエリア「板橋のiカリキュラム開発重点校」研究授業（第2回目）が、板橋第一中学校で行われました。教育のための科学研究所からは、新井紀子代表のほか、菅原真悟上席研究員、犬塚美輪学芸大学准教授（教育のための科学研究所客員研究員）が参加し、各科目の研究授業の参観、助言を行いました。

研究授業のひとつである中学2年生の数学は、一次関数が題材でした。関数は中学生にとって最も理解が難しい内容のひとつで、一次式と一次関数の区別がつかない生徒も少なくありません。教育指導要領が求める「数学を使うことの良さ」を実感させることもなかなか難しい単元です。

本授業では、教育のための科学研究所からの事前助言に基づき、3つの問いから始まりました。

次の文章のうち、「変化する2つの量」の関係が「一次関数」になっているものはどれかを考える問いです。

1. ダイエットに挑戦したが、体重が増えた日もあれば減った日もあった。
2. ひまわりの種をまいたところ、芽が出てからしばらくはなかなか成長しなかったが、その後ぐんぐん成長し、花が咲くころに成長が止まった。
3. 冷たいペットボトル飲料をある保冷バックに入れて持ち歩いたところ、その飲料は時間がたつにつれてほぼ一定の割合で温度が上がることがわかった。

クラス全員が３が一次関数であると手を挙げました。

授業者はここで流すことなく、（１）なぜ３は一次関数だと思ったのか、（２）１と２はなぜ一次関数ではないと思ったのか、を生徒から文章で引き出していました。これは、具体例同定（理数）の活動として位置づけられました。

「３は時間に対して一定の割合で温度が上がるので一次関数になる」「１は時間に対して体重が一定の割合で増えても減ってもいないので一次関数ではない」「２は時間に対してひまわりの成長が一定でないから一次関数ではない」

ただし、２について「変化する２つの量」が何かがわからない生徒もいました。「ひまわりの高さ」が明示的に文中に書いてないので迷うようです。このように、ふつうに書かれている文章の中で、着目すべき数量が何かを取り出すこと、そして、その関係を式で表すことの良さ（＝未来や過去を予測できる）を感じてほしいと思います。

次に授業者はプリントを配布しました。そこには、実際にペットボトル飲料の温度がどのように変化したかが表になっています。

分	20	30	40	50	60
℃	5.2	5.8	6.4	6.9	7.6

まず、「変化量」を見ます。小数が入る2桁の引き算を4回しなければならないのですが、結構時間がかかりました。やはり小学校で3桁の計算までは苦労なくできるようになって中学校に進学しておくと、中学校の授業では概念理解に集中できますね。適度な量のドリル、そして中学入学後も一定量の四則演算ドリルは必要だということがわかります。

さて、差分は、0.6, 0.6, 0.5, 0.7になりました。平均すると「10分ごとに約0.6度上がる」と言えるというところまでは全員が納得できました。ところが、「1分（１単位）ごとにどれだけ変化するか」がなかなかわかりません。

「10分で0.6度上がる」⇔「1分で0.06度上がる」

の変換が難しいようです。これはRSTでは「同義文判定」に位置付けられる内容です。

このあと、表をグラフで表し、式にしていきます。その際、教科書に書かれている一次関数の定義を振り返ります。

一次関数とは$$y$$を$$x$$の一次式で表せる関数のことである。 $$ y=ax+b $$ $$a,b$$は定数

この定義を正確に理解するのが極めて難しいことが、RSTのこれまでの結果からわかっています。

まず、$$a,b$$は定数という但し書きを読まずに、前提なしに「$$ax+b $$」という形の式は一次式だと勘違いする生徒（学生）は東大生にも少なくありません。また、「$$y$$を$$x$$の1次式で表せる関数」を正しく読解できる生徒は少なく、その後に書いてある$$ y=ax+b $$を一次式だとほとんどの生徒が読みます。正しくは、$$a,b$$は定数のとき$$ax+b $$は一次式であり、そのような$$x$$の一次式として$$y$$を表せる、つまり$$ y=ax+b $$と表現できるとき、一次関数といいます。

このように解像度高く読まないと、数学では様々な概念を混同してしまいますので、注意が必要です。授業者には、生徒の興味関心を引くだけでなく、解像度高い読解を促すような問いかけも意識してほしいところです。

プリントで示された表には初期値、つまり最初の温度が書かれていません。20分後からの表だけです。$$x=20$$と$$x=60$$の$$y$$の値から、連立方程式で式を求めるか、変化の平均値が1分ごとに0.06度であることから$$ a=0.06 $$は得られているとし、20分後の値から一次方程式を解くことで、切片である$$b$$を求めるなど、いくつかの方法で生徒たちは、求めるべき式、

$$y=0.06x+4$$

を導出しました。一人ひとりだとなかなか難しかったので、隣どうしで話し合いを行うことで計算間違いを見つける等の手がかりを得て、式にたどり着けた生徒が多かったようです。ここでも小数のある計算、特に割り算に中学2年の段階でも課題が残っていることがわかりました。

こうして、「ペットボトルの中の飲料は、時間を$$x$$としたとき、温度yは$$ y=0.06x+4 $$という式に従って上昇する」というまとめで授業は終わりました。

ここで、新井が手を挙げて、こんな問いかけをしました。

では、1600分後には、ペットボトル飲料は沸騰しますか？

これは生徒も想定外だったようでざわつき、「そんなことにならない」と言いましたが、「だとしたら、それは特定の$$x$$の範囲においてのみ一次関数である」ということに気づいた生徒もいたようです。次回の展開が楽しみです。

 

※冒頭の「ひまわりの成長」についての文章はもう少し詳しく書いたものを、2011年に実施された日本数学会第一回大学生基本調査のプレ調査として2010年に行われた調査で「ひまわりの成長を適切に横軸と縦軸をとって、概形を表しなさい」という問題として出題しました。教員養成系大学で大変悲惨な結果になったことが思い出されます。