タグ:研究授業
新潟県燕市で講演・講評を行いました。
新潟県燕市では、令和3年度から市内全小中学校において、汎用的基礎読解力の診断のためにRSTを導入しています。
2022年11月22日に燕市教育委員会主催の「令和4年度 読解力育成プロジェクト全体研修会」が燕市立燕西小学校を会場として開催されました。まず、開催校である燕西小学校の6年生の算数において、特に「イメージ同定」を意識した授業として、「同じ形ってどんな形?~暮らしに生かす拡大図と縮図~(全 12 時間)」の仕上げに相当する発展的な授業が展開されました。市内すべての小中学校から多くの先生、教育長はじめ教育委員会の指導主事が見守る中、体育館で授業が始まりました。
燕西小学校では、毎年、小1~小6が班をつくり、遠足をします。同じ起点と終点ですが3つコースがあります。そのコースのうち「田んぼコースが一番長いらしい」ということを児童は実感(時間がかかる、疲れる)などから感じています。それが本当かどうかを地図の縮尺を用いて確認し、「どれだけの道のりの差」があるかを数値として確認するという大変意欲的な内容でした。
児童の「実感」とこれまで学んできた「縮尺」をつなげることにより、「縮尺で考えることの良さ」を実感させるという意味では、「考える力を育てる」「算数・数学の考え方の良さを実感する」という学習指導要領の目的に合致した、内容の濃い授業です。ただ、イメージ同定と推論の力はもちろんのこと、作業に集中力が求められる授業であることに注意が必要です。
1.地図上のジグザグの道を線分に区切り、コンパスで取り、直線上に移すには、コンパスの使い方の習熟が必要。
2.「どこまでは測り済みで、どれはまだ測っていないか」をチェックする注意深さが必要。
3.地図が1万9800分の1の地図だったため、「本当の長さ」を計算するには3桁以上の掛け算の能力が必要。(学習指導要領外)
3については最初から電卓またはタブレット上の電卓を使うか、2万分の1の地図を用いることで3桁どうしの掛け算を回避できるようにする工夫があるとよいでしょう。
さて、講演では「リーディングスキルに着目した授業づくり」というお話をさせていただきました。
「すべての児童(生徒)にとって、すばらしい授業」というのは存在しません。たとえば、RSTの能力値が4~5に固まっているような学校では、上記のような授業はまさに児童にとって「算数の良さ」を実感できる授業になることでしょう。一方、RSTの能力値が2.5を平均として分布しているような場合は十分な効果が得られないかもしれません。
リーディングスキルを「伸ばす授業」というのは、能力値が1の子を2に、2の子を3に、3の子を4に、4の子を5に上げ、平均を上げつつ分散を小さくする授業です。自分のクラスの子のRSTの能力値を把握した上で、「全員が手を挙げられる問題を3つ」「半数が手を挙げられる問題を2つ」「能力値が一番高い層が手を挙げられる問題を1つ」準備し、一斉授業の中で、それぞれが確実にRSを昨日より今日、今日より明日、少しずつ上がるような授業を目指すのが、(地味ではあるが)最も効果があるのではないか、というお話をしました。
※「問題」というのは、根拠をもって解決されるべき問題を意味します。(例:「軽井沢の6月の平均気温は何度ですか?」(雨温図を読む、イメージ同定)、「ゆうなさんは『土地の高いところでは、気温が低くなる』と言っています。どのグラフを見てそう言っているのでしょう?」(雨温図を読む、イメージ同定)) 「感じたこと・思ったことの表出」は上記の「問題の数」とは別でお考えください。
意欲的・発展的な授業でなくても、リーディングスキルは、工夫によって上げることができます。頑張って計画した特別な授業より、むしろ日々の「ふつうの授業」が大切です。教科書見開き2ページの本文・資料を最大限活用しましょう。文の基本構造の把握が弱い子には、本文の構造の確認を(文法的に、ではなく自然に)確認してください。DEP、ANAはできているが推論が弱い子には「〇行目に・・・と書いてあるね。なぜだろう」のように根拠を聞きましょう。その際、根拠としてまずは教科書に書いてあることを挙げられるようにしたいですね。(もちろん、児童の実感や経験とつなぐ活動も大切ですが。)そのような実践ができている学級では、「今日学習する教科書のページ」を全員が開いており、先生が質問をすると、教科書から答えを探そうとするので、どれだけ日々の実践ができているかが一目でわかります。
RSTを導入していらっしゃる他の自治体でもご参考になれば幸いです。
板橋区立板橋第一中学校での授業実践(中2地理)ーその3
6月15日、板橋区立板橋第一中学校の2学年の社会科で、「教科書を読み解きながら期末テストに備える」授業をしました。
その1では、教科書見開き2ページからの検索課題の指導法をご紹介しました。中学生でも教科書の「使い方」が身に着いていない生徒が少なくないことを実感していただけたのではないかと思います。その2では第二次・第三次産業の定義、及び教科書の資料部分を活用して、身近な企業を第二次・第三次産業に根拠をもって分類する具体例同定の指導法を取り上げました。今回は、RSTでいうところの「イメージ同定」の力を測る問3についてご紹介します。
RSTや「読み解く力」では、説明文に掲載されている非テキスト情報を「イメージ」と呼びます。グラフ・表や図、説明的なイラスト、年表、数式、譜面などがイメージに含まれます。テキスト情報とイメージと正しく結びつける力を「イメージ同定」と呼んでいます。
問3.他の工業地帯と比べたとき、中京工業地帯の特徴(とくちょう)を3つ文章で挙げなさい。
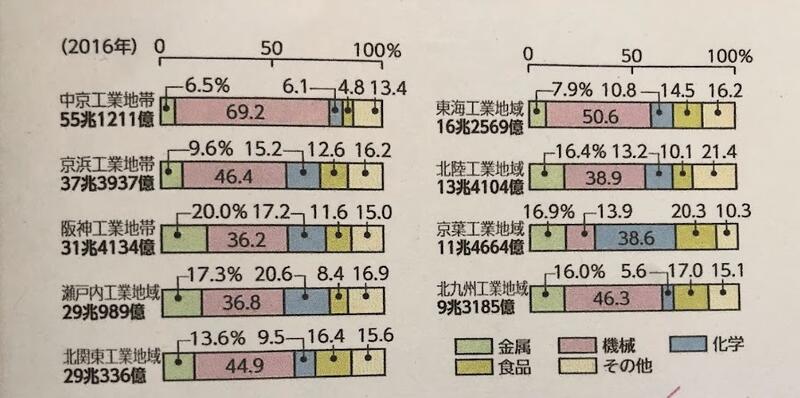
教科書の本文には、一般的な第二次産業の特徴については書かれていますが、中京工業地帯については書かれていません。(中京工業地帯の詳しい特徴は、実は小学校5年生で習います。こちらの授業の前後に学びます。)この問題は本文ではなく、教科書に掲載されている資料3「日本の工業地帯・工業地域と出荷額の割合」の帯グラフ、円グラフ、地図を読み解いて答えなければなりません。特に次の図が重要になります。
(教育出版「中学社会 地理 地域に学ぶ」169ページ、「日本の工業地帯・工業地域と出荷額の割合」より)
教科書の該当箇所で「中京工業地帯」の文字が出てくるのは、資料3だけなので、まず「検索」の力でこの図にたどり着けるか、が最初の関門になります。本文ばかり見ている生徒には「見開き2ページで『中京工業地帯』というキーワードが出てくるのはどこか、探してごらん」を促します。資料3に目が行ってしばらくしても手が動かないときは、「帯グラフのどれが中京工業地帯かな?」と尋ね、中京工業地帯の帯グラフに注目できているか確認します。
その上で、尋ねます。「ぱっ、と見て、中京工業地帯の特徴で気づくことはない?」と。
すると、多くの子は「ピンクが多い」と答えます。
「ピンクってなんだろう?」と尋ねると、「わからない」という答えが多く聞かれました。
グラフの右下に、緑は金属(工業)、ピンクは機械(工業)と読み方が書いてあるのですが、そこに至れない生徒が少なくないのです。ひとりも取り残さない教育を目指すなら、グラフの読み方を、教科書を使って、繰り返し指導する必要があることがわかります。
「ここに色分けの意味が書いてあるよ」と指すと、「あ。」とつぶやき、文章を書き始めることができました。
さて、答え合わせです。
「機械が多い」
これを書いた生徒が多数いました。しかし、これでは、「中京工業地帯には機械が多い」のか「中京工業地帯には機械工業の会社が多い」のか「機械工業の生産量が多い」のか「機械工業に従事する人の数が多い」のか、わかりません。では、わかるようにするにはどうしたらよいか。
そこで、小学5年生のときに習った(はずの)帯グラフの読み方をとり出して指導しました。
1.グラフのタイトルは何か。単位は何か。
2.全体を見て、わりあいがいちばん多いのはどれか。
3.増えているもの、減っているもの、変化がはげしいものはどれか。
4.全体の数字はどのように変化しているか。
5.共通していえることはないか。
6.全体のけいこうから、これからの変化を予想できるか。
(東京書籍 新編「新しい社会5下」6ページより)
帯グラフには、複数のものを比較する場合と、経年変化を見る場合があります。3,4,5,6は後者のための「読み方」で、1,2が今回必要になる帯グラフの読み解き方です。
資料のタイトルは「日本の工業地帯・工業地域と出荷額の割合」です。ですから、多いのは「出荷額」でしょう。(残念ながら、教育出版のこのグラフには「単位」が書いてありません。改善を期待します。)ピンク(機械)が多い、ことを表現するには、グラフのタイトルから「出荷額(にしめる)」「割合」という言葉をもってきて、先ほどの答えを補います。
「出荷額にしめる機械工業の割合が大きい。」
このように書ければ正解です。「出荷額にしめる機械工業の割合が、5割に近い。」などもよいでしょう。
多い方に注目したら次は、少ないものにも注目します。すると、ブルー(化学)や黄色(食品)が少ないことに気づきます。もう「ブルーが少ない」と書く生徒はいません。
「出荷額にしめる化学工業の割合が小さい。」
「出荷額にしめる食品工業の割合が小さい。」
などを挙げることができました。全体をながめたときに気づくのが、中京工業地帯の出荷額全体の多さです。
「日本で一番出荷額が多い工業地帯である。」
「どの工業地帯・工業地域より出荷額が多い。」
のように自発的に書ける生徒が多くいました。
ところで、資料3の地図と本文にひっぱられたのか「太平洋ベルトにある」と書いた生徒がいました。これは不正解です。なぜなら「他の工業地帯と比べたとき、中京工業地帯の特徴を挙げなさい」と問われているので、他の工業地帯と「異なる点」を挙げなければいけないからです。他の工業地帯の多くも太平洋ベルトにあります。
これで問1~問3まで答え合わせができました。最後に私は次のように語りかけました。
「問3はテストで配点が高い問題です。問3をスラスラ書けたら日比谷高校も夢ではありません。さて、問3は『頭が良くて、才能がないと』解けない問題だったでしょうか?いいえ、違います。『ピンクが多い』『ブルーが少ない』ということがわかり、グラフの読み方を覚えれば誰もが書くことができますね。誰もができるはずのことをきちとできれば日比谷高校に合格できる、ということです。」
ここで「よっし!」とこぶしを突き上げる元気な生徒が数名いました。
「ただし、『機械が多い』と『出荷額にしめる機械工業の割合が大きい』と書けるかどうか、その差が今の君たちと日比谷高校に入学した生徒の違いでしょう。」
すると、「あー、やっぱりだめか・・・」という落胆する声が聞こえます。
「大丈夫です。なぜなら、高校入試は明日ではなく1年半後にあるからです。今日から、基本の教科書の読み方、グラフや表の読み方をしっかり身に着けて学習すれば、きっと望む学校に入学することができるでしょう。」
もう一度「よっし!」と元気に言ってくれてよかったです。
今回の授業で、私はひとつも「社会科のコンテンツを教える」ということはしていません。面白い話もしていません。ただ、教科書の読み方、グラフの読み方のコツを伝授しただけです。
中学校は義務教育の総仕上げの時期です。先生方には、コンテンツを教え込むことから、じょじょに生徒の自学自習に伴走する学習支援者を目指してほしいと思います。そして、すべての子が「自学自習するスキル」を身に着けて卒業してほしいと願っています。自学自習のベースは、「説明文を読み解く力」と「説明文を書く力」です。それらは、特別な才能がなくても、適切な指導と学ぶ機会があれば(自動車の運転免許を得るのと同じように)身に着くはずの力です。そして、「学校」は、まさに、そのようなスキルを着実に身に着ける場所として、社会に存在しているのではないでしょうか。
今回はワークシートの問4にたどり着くことはできませんでした。私は、外部講師ですから、事前にその日授業をするクラスの状況を把握することはできません。その日、子どもたちと接して、「今日はどこまでやるか」を冒頭3分くらいで決めます。今回は、冒頭で「今日は問1から問3まで一緒に解いていきましょう」と宣言しました。(他の学校では、問2まで、あるいは問1だけ、にしたかもしれません。)
ただし、問4について話はしました。「問4をスラスラ解けるようになったら、東大に入れます」と。根拠があります。東大文系の最難関は社会科の問1の600字の大論述です。そして、東ロボプロジェクトの経験から、多くの東大合格者はその600字の大論述が「大してできていない」ことがわかっています。ですから、中学2年の段階で問4が解けるようになれば、東大合格は夢ではないのです。
そう話すと、子どもたちは、大変驚くと同時に、「どういう状態を目指して勉強していけばいいか」のイメージが多少は掴めたようでした。
※ちなみに、「ドラゴン桜」ではありませんので、日比谷高校→東大に行くことを子どもたちに目指させることが良いと思っているわけではありません。ただ、「ふつうにやればできること」なのに「とんでもない才能がないと無理なこと」だと思わない方が、人生の選択肢は増えると思っているだけです。
板橋区立板橋第一中学校での授業実践(中2地理)ーその2
6月15日、板橋区立板橋第一中学校の2学年の社会科で、「教科書を読み解きながら期末テストに備える」授業をしました。
その1では、ほぼ全員に解いてほしい問1の指導方法についてご紹介しました。今回は第二次産業、第三次産業の定義を読んで、具体的な企業をどちらかに分類する課題です。教科書では二次産業を次のように定義しています。
原材料を採掘したり、加工したりして製品をつくり出す産業を第二次産業といい、主なものに工業があります。(教育出版「中学社会 地理 地域に学ぶ」168ページ、9~11行目)
分類するのは、こちらの企業です。
問2. 次の企業を第二次、第三次産業に分類しなさい。
ユニクロ、日清食品、ソフトバンク、東京電力、ローソン、パナソニック、みずほ銀行、住友金属鉱山、積水ハウス、JR東日本、ヤマト運輸
正式名称ではありませんが、CM等で子どもたちに馴染みがある略称で出題しました。
定義に従って具体的なものを分類する力を、RSTでは「具体例同定」力と呼んでいます。穴埋めプリントに「第二次産業」「第三次産業」と正しく埋められても、現実社会に応用できないようでは知識とは言えません。「あの企業は二次産業。なぜなら・・・だから」と言えるようになってほしいものです。
学校ではあまり問われないタイプの問題なので、最初の一歩が踏み出せない生徒が少なくありませんでした。が、「1つでも当てれば2点だと思って、どれかひとつでも選んで書いてごらん。白紙だと0点だけど、書けば当たるかもしれないよ」と後押しすると、多くの子が「みずほ銀行」を選び、第三次産業に分類しました。銀行は「原材料から製品をつくり出しているわけではない」からです。ひとつ書くと、次々に書き込める子が増えていきました。
答え合わせの時間には、それぞれの企業が第二次、第三次のどちらに属するのか、その理由は何か、みんなで議論しました。
日清食品は、子どもたちに馴染みのある、あの「カップヌードル」を出している企業です。ただ、子どもたちは「工業」というと真っ先に機械工業をイメージするらしく、「第三次産業だと思う」側に手を挙げた生徒が1/3ほどいました。そこで、169ページの「日本の工業地帯・工業地域と出荷額の割合」の帯グラフに注目させました。工業の中の割合を見ると、「金属、機械」のほかに「化学、食品、その他」があることがわかります。ということは、食品工業という種類が工業の中にある、ということです。日清産業は、「小麦粉などを原材料として、麺に加工しているから、第二次産業」という根拠をもって、分類することができました。
「住友金属鉱山、という会社を知らない」という子はたくさんいました。実は、私も詳しくは知りません。(住友金属鉱山さん、ごめんなさい)すると、「名前に『鉱山」と書いてあるから『鉱業』ではないか」という生徒が出て、他の生徒も納得して第二次産業に分類できました。
「積水ハウス」は、第二次・第三次半々に分かれました。「絶対に第二次」という生徒に理由を聞くと、「168ページのグラフ2『日本の産業別人口構成の移り変わり』に第二次産業は『鉱業、建設業、製造業』と書いてあって、積水ハウスは建設業だから」とパーフェクトな答え。本文ばかりに注目していた生徒たちが一斉にグラフ2に注目し「ああ、そうかぁ」「そこに書いてあったのかぁ」と言う様子は微笑ましかったです。
「東京電力」はどうでしょう。さきほどの箇所に注目すると、「第三次産業…電気・ガス・水道業、情報通信業、運輸業、卸売業、小売業、金融業、保険業、宿泊業、飲食サービス業、生活関連サービス業、教育、学習支援業、医療、福祉など」の冒頭に「電気」とあります。ですから、東京電力は第三次産業だということに気づけました。ここまでいくと、あとはすいすい進み、ヤマト運輸は運輸業、ソフトバンクは情報通信業、パナソニックは製造業、JR東日本は運輸業、ローソンは小売業のように分類できました。
みんなが最後まで悩んだのがユニクロでした。ユニクロは小売業なのか、製造業なのか。どちらに重きがあるのか。(私も悩んだので事前に調べました。登録は第二次産業だそうです。)
そういう中で、流通やIT、グローバル化が進む中で、第二次と第三次の境界があいまいになっていること、場合によっては、「2+3=5の5次産業」などと言われることがあることなどを話しました。
「今日から、商店街を歩いていても、CMを見ても、『あの店は第二次産業』『あの会社は第三次産業』と考えられるようになるといいね」と話し、「ところで、伊藤校長先生は第何次産業に従事していますか?」と聞くと、「第二次、生徒を生産しているから」(←原材料が何か、という部分が抜け落ちてますね。)と言ったり「学習支援業だから第三次産業」と言ったりする子がいて、まだ少し混乱もあるようです。「校長先生は教育業に携わっているので、第三次産業従事者です。学習支援業は塾です」と言ったら、「そうか!」と納得した様子でした。
****
この部分については、10数人で見学にお越しになった立山町の先生方から「教科書をまさに『使い倒す』授業でした」との感想が多く寄せられました。
追記:参観していた教員からは、「積水ハウスの分類で、もっと生徒の考えを引き出して議論させてもよかったのではないか」とのご意見がありました。そのような学習活動が推奨されていることは私も認識しています。一方で、企業の分類、産業の分類には定義があることなので、(自分の考えは一度置いておいて)定義に従う、ということも「学ぶ基礎」として重要かと思います。
板橋区立板橋第一中学校での授業実践(中2地理)ーその1
6月15日、板橋区立板橋第一中学校の2学年の社会科で、「教科書を読み解きながら期末テストに備える」授業をしました。
板橋第一中学校は、板橋区が推進する「義務教育9年間で子どもたちに、『読み解く力』を育成し、学力向上を図る」ことを目的として考案された「i-カリキュラム」の学びの重点校のひとつです。4年前から学校一丸となって「読み解く力」育成の授業改善に取り組んでいます。
その一環として、令和3年度から社会科の一部で、定期考査を「教科書持ち込み可」にするという試みが行われています。生徒は「教科書持ち込み可」を歓迎しますが、平均点を比較すると、実は教科書持ち込み可のテストの方が成績は奮いません。なぜでしょう。
定期テストの範囲は見開き10ページ以上あることがほとんどです。テストが始まってから、初めて教科書を読むようでは、時間内に問題を解き終えることはできません。事前に教科書を読み解き、どのページにどんなことが書いてあるか把握した上で、内容が腹落ちしていていないと、「読み解き、記述する」テストには対応できないのです。しかし、ひとりで事前に教科書を読み解ける生徒は少数です。
そこで、今回は、期末テストの準備として、期末テストの範囲から見開き2ページに絞り、どんな風に教科書を読み解き、問題を解けばよいか、その方法を伝授しました。今回、読み解く対象に指定したのは、教育出版の「中学社会 地理 地域に学ぶ」の168~169ページ、「日本の産業活動と立地」です。
写真1:貿易の自由化の参照表現について指導しているところ。指で指している箇所が「貿易の自由化」
授業の冒頭でワークシートを配布しました。板橋区1年生持ち込み可問題2022年.pdf
彼らが経験した中間テストのボリュームから考えると、問1~問3は15分で解きたいところ。該当箇所を開き、15分にタイマーを設定し、解き始めました。この記事では、クラスの大半に解いてほしい問1の指導法についてお伝えします。
*****
問1の1「貿易の自由化とは何か。25 字以上 30 字以内でかきなさい。」
これは、「教科書の構造を理解しているか」「検索できるか」という、学習基礎スキルを問う問題です。「貿易の自由化」というキーワードは教科書に太字で書かれています。但し、本文には定義は書かれておらず、「貿易の自由化」の言葉の右上にピンクで①と書いてあります。同じページの左下に同じくピンクの①があり、それが「参照先」で、次のように書かれています。
ものやサービスの輸出入には国境を越える時に関税(税)がかかることがほとんどです。この関税や輸入の制限などをやめて、自由な貿易を行うようにすることを貿易の自由化といいます。(教育出版「中学社会 地理 地域に学ぶ」168ページ註①より)
机間巡視すると、教科書の「参照表現」を知らないせいで第一問からつまずいている生徒が半数ほどいました。
「貿易の自由化の右肩にピンクの①と書いてあるよね。これ、なんのマークか知っている?」と聞くと、「知らない」とのこと。「ピンクの数字がついている言葉の説明が、同じピンクの数字の先に書いてあるよ。見てごらん」というと、「えー、そうなんだ」と驚いているようでした。大人にとっては、当たり前の「教科書の使い方」でも、児童生徒は教えてもらわないとわからないことがあるのです。
答え方も具体的に指導する必要があります。
「~とは何か」と問われたら「・・・・こと」と書きましょう。
「~とは何か」は定義を聞かれているので、「・・・・すること」「・・・・のこと」のように、最後が「こと」で終わるように書くとよいです。この「型」を覚えておくと、「・・・こと」と書かれた部分を探せるようになりますし、この型にはまらないようなものは答えではない、と排除することができるようになります。
問1の1の答えは参照先をそのまま引用すると、「関税や輸入の制限などをやめて自由な貿易を行うようにすること」(29字)です。
問1の2「貿易の自由化が日本の農業にとってなぜ打撃になったのか、そのわけを 15 字以上 20 字以内でかきなさい。」
全員、貿易の自由化の周辺に視線が向いています。そこには、以下のように書かれています。
貿易の自由化が進んで、国内より低価格の農産物が輸入されるようになると経営は厳しくなります。農業で働く人の減少や高齢化、後継者の不足も課題になっています。こうした状況もあって、農業で働く人は、東京や大阪などの大都市から離れた、地方に多いという特徴がみられます。(教育出版「中学社会 地理 地域に学ぶ」168ページ本文4行目~9行目)
ここで答えが大きく2つに分かれました。「国内より低価格の農産物が輸入されるようになるから」を選ぶ生徒と、「農業で働く人の減少や高齢化、後継者の不足」を選ぶ生徒です。前者が原因で、後者は結果です。「わけを書く」のように原因の記述を求められているのに、結果の方を書いてしまう生徒がいるのです。このようなときにも「型」の指導は有効です。
わけ(理由)を書くときは「・・・から」と書きましょう。
「国内より低価格の農産物が輸入されたから、経営に打撃を受けて、(その結果)農業で働く人の減少や高齢化、後継者の不足が起こった」ので、前者が選ぶべき箇所だということがわかります。RSTでは推論(INF)能力に該当する箇所です。
ただし、「国内より低価格の農産物が輸入されるようになるから」あるいは「海外から低価格の農産物が輸入されるようになるから」と書くと字数制限に収まりません。意味を変えずに言い換える能力(RSTでは同義文判定(PARA))が必要になります。縮約(約め方)の工夫を具体的に指導しました。
「されるようになるから」を「されるから」と約めると5文字減って、字数制限に収まります。他にも「低価格」を「安い」、「海外からの農産物」を「海外産農産物」にすることで、意味を変えずに字数を減らすことができます。
生徒たちに次のように問いかけてみました。
「問1は『頭がいい人』や『社会科が好きで得意な人』や『文章が巧い人』だけができるかな?」
そうではありません。教科書の使い方を知れば、そして、約め方のやり方を工夫すれば、誰でもできる、ということを生徒たちは実感できたようです。実際、下校する生徒たちに校長先生が授業の感想を聞いたところ、(「楽しかった!」という感想が多かったのは嬉しいことでしたが)「教科書の読み方がわかった」「答えの書き方がわかった」と言う子が多かったそうです。
この記事をお読みの教員の中には、「そういう指導はもちろんしている」と思う方も少なくないでしょう。教科書の使い方や読み方、答えの書き方は、一度や二度の指導ではなかなか身に着きません。何度も実践し、失敗しながら上達していく過程が必要なのです。
では、その2に続きます。
追記:
この記事をお読みになった方の中には、「紙の教科書だから参照表現を理解しなければならなくなる。デジタル教科書にハイパーリンクを埋め込んでおけば、ワンクリックで参照先に飛べる。だからデジタル教科書の方が良い」と思う方もおられるでしょう。しかし、ハイパーリンクは認知負荷が大きく、本文の理解を阻害するとの研究結果がこちらの論文を始めとし、いくつも出ており注意が必要です。
実際、デジタルコンテンツで学ぶ児童・生徒を見ていると、「詳しく知りたいからリンクをクリックする」というより、「目立っているからクリックする」「厭きたから(何らかの気分転換をしたくて)クリックする」ことの方が多く、「この画面の前に何を見ていた?」「何を調べようとしてクリックしたの?」と聞くと「わからない」と答えることが圧倒的に多いのが現状です。
追記2:
小中学校の授業で、「自分の言葉で書きましょう」「自分の意見を言いましょう」という指導が徹底されているためでしょうか。教科書から「抜き書き」するのはいけないことだ、と思う生徒が少なからずいます。「教科書を読み解いて自分のものになったら、抜き書きしても自分の言葉になるんだよ」というと安心した顔をするのが印象的でした。
追記3:
この記事をお読みになった複数の方から、「なぜ中学生になっても教科書の凡例がわからないのか。読書量が足りないからではないか」との疑問が寄せられました。私たち大人でも、Excelの滅多に使わない機能や、自分が契約している保険がどこまでをカバーしているか、等を知らずに生活していることは多いです。なぜでしょう。滅多に使わず、意識に上らないからではないでしょうか。
「本文だけでなくグラフや表、地図、コラムや実験の注意事項も含め、教科書を毎日使い倒して」いれば、どの子も教科書を使えるようになります。一方、プリントやワークシート学習を中心にしていれば教科書の使い方が身に着かないのは当然かと思います。
板橋区学びのエリア「板橋のiカリキュラム開発重点校」研究授業が実施されました。
12月3日、板橋区の学びのエリア「板橋のiカリキュラム開発重点校」で令和2年度、3回目となる研究授業が実施されました。今回は、板橋第二小学校での小学5年生社会科の研究授業の様子をご紹介します。
今、板橋第二小学校の5年生の社会科では、日本の工業生産の中盤にさしかかっているところです。科学技術立国といわれる日本において、どんな工業が誰によってどのように支えられているのかを5年生の段階で理解をしておくことは、日本がこれからどのような国になっていくのか、また、自分がその国でどのような産業の担い手になっていくのかを想像する上でも重要な単元です。
今回の研究授業では、「小学社会5」(教育出版)の156ページ~157ページを学びます。この授業案を考案した山田禎文先生は、この2ページを何度も何度も読み込んだそうです。
高学年になると教科書は抽象度を増すだけでなく、異なるレイヤーの資料が見開き2ページに詰め込まれていることがわかります。黒で囲まれているのが本文、それ以外に青で囲んだ資料、薄い青で囲んだコラム、ピンクで囲んだ「強調したいポイント」(ただし、まとめではない)、加えて、緑で囲んだ「問い」があります。資料にも、統計のグラフや表、地図、そして本文の一部を強調するための写真やイラスト、歴史の場合には当時の風刺画なども含まれています。
教科書の本文を読み解くことが難しい児童にとって、このような本文と資料の関係性を把握することはさらにハードルが高いことです。そして、それはまさに近年重視されている「多様な資料を参照しつつ、自らの考えをまとめていく」PISA型読解力は、まずは教科書の見開き2ページを十分に活用して読めるようになること、から身に付けていくべきでしょう。
さぁ、この2ページの「読解」を山田先生はどのように設計したのでしょう。授業に沿って、紹介したいと思います。
今日のめあては「大工場と中小工場のちがいを知り、中小工場の特色や役割を読み取ろう。」です。
めあてを最初に書くことは、どこの教室でもしていることでしょう。ただし、山田先生の方法は、他と少し違います。「よく聞いて。今日のめあてはいつもより少し長くて難しい。だからしっかり聞いて書き始めよう」
つまり、声でめあてをはっきりと伝え、その意味を児童に考えさせて(頭の中で文字に変換させて)自力で書き始めさせるのです。児童が書き始めたのを確認した上で、山田先生はめあてを黒板に書き始めました。
山田先生のクラスでは日頃からそうしているようで、めあてを「聞く」ということに児童が「全集中」していることがわかります。これまで多くの教室で、めあてを先生が書き終わるのを待ってから、ただの文字列として児童・生徒が写している情景を見てきた私にとって、このクラスの「音としてめあてを聞いて、それを仮名漢字交じりの文章にする」集中度の高さが強く印象に残りました。こんなところからも「読み解く力」は育成できます。どのクラスでもその気になれば取り組めることではないでしょうか。
めあてを書き終えた後、山田先生は驚くべきことを児童に問いかけました。
「今日の授業のめあてが『大工場と中小工場のちがいを知り、中小工場の特色や役割を読み取ろう。』だとすると、今日の授業ではどんなことを学習しないといけないのかな。」
めあてから授業で何を学習すべきかを児童が考える、というのは究極のアクティブラーニングではないでしょうか。そのためには、もちろん事前に授業の全体設計をし、めあてから児童でも授業計画ができるように練っておく必要があります。
このめあてから、自然に2つの達成目標が導出されました。
- 大工場と中小工場のちがいを知る。
- 中小工場の特色や役割を読み取る。
「めあてを単に分解しただけではないか」と思う人もいるでしょう。いいえ、そんなことはありません。小学5年生の半数は、複文を単文に箇条書きで分解するだけでもつまずくのです。児童が今日すべきことを意識した上で、その2つを達成しようと思う、この小さなことが、この授業で児童が最後まで集中力と途切れさせない上で、鍵になっていたように思います。
めあての第一「 大工場と中小工場のちがいを知る。」に取り掛かります。
次に、山田先生は子どもたちにゆさぶりをかけていきます。
「大工場か中小工場か、というのはどこで決まるのだろう?」
- 面積で決まる。
- 働く人の人数で決まる。
- (生産額で決まる、生産量で決まる、を入れてもよいかもしれません。)
挙手をさせると、面積で決まるという児童が何人かいました。人数で決まると言った児童も明確な根拠があるわけではないようでした。
そこで、山田先生は、「実はその定義は教科書の156ページに書いてある。どこに書いてあるか探してみよう」と指示しました。興味深いことに、成績下位の児童ほど、まず本文をべったりと読んで答えを探そうとします。目の前に「キーワード」として中小工場と大工場の定義が書いてあるのに、気付きません。成績下位の児童は教科書の「構造」が十分にはよくわかっていないようです。
指導者が「書いてあるのだから、誰でもわかるはず」との先入観をもたずに、実際に探させることで、「定義だから、『中小工場とは・・・、大工場とは・・・』と書いてあるはず」と見当をつけて探そう、という基本的学習スキルとしての検索が身に付くようになるのです。具体例同定に着目した指導です。
「わかった人はいますか?」の呼びかけで、手を挙げた生徒が数名いました。ですが、山田先生はすぐに答えを言わせずに「どこに書いてありましたか?」と尋ねました。「キーワードに書いてありました」との返事を受け、「そうだね。キーワードに書いてあったね」とクラス全員で共有すると、成績下位の子も「ああ」「あ、そうか」などと声をもらし、定義を書き始めました。
教科書上の資料から、「働く人が1~299人までの工場を中小工場という。」「働く人が300人以上の工場を大工場という。」をクラスほぼ全員が「どこに書いてあるか」を認識した上で書くことができました。
山田先生は「文章になっているかな?『という』『です』までしっかり書こう」と促しました。これも、読み解く力の出力の質を高める上で重要な指導です。実は、文章で書けるか、キーワードでしか書けないかで、高学年はどの科目でも大きな差がでます。キーワードを書けているからわかっているだろう、と流さずに、「文になっているか、なっていないか」は繰り返し指導したい点です。
(文になっていない部分を指摘され、「です」を付け加えて文章化している途中のノートの様子。ただし、「働く人が300人以上の工場を大工場です」では文にならないので悩んでいるところ。このようなつまずきを予想し、表現方法をクラスで共有することで、表現のバリエーションが各自の中で蓄積されていきます。学びのコミュニティの中で学んでいく一斉授業の良さのひとつです。)
その上で、「実は働く人が1~29人の工場を小工場というそうです。中工場はどんな工場かな?」と聞き「働く人が30人~299人までの工場を中工場といいます」と答えさせていました。
算数と社会の科目横断が実現されている、良いシーンでした。
次に、まためあての1を確認し、「違いを知るために、156ページの下の帯グラフを見て、中小工場と大工場の違いを文章で書いていこう」というイメージ同定に相当する活動を行いました。RSTでは文から正しい図を選びますが、それはテストの形式上のことに過ぎません。図から正しい説明文を書くというのもイメージ同定のむしろ高度な活動です。
グラフの特徴を3つ挙げるという課題を与えると、比較的成績の良い児童はグラフを順番に見て、効率よく特徴をあげていきます。一方、中位層以下は、グラフ全体をぐるぐるみていて視点が定まらず、迷っているうちに時間を浪費しがちです。中位層以下には机間巡視の際、「まず最初のグラフからわかることを文にしてみよう」などとアドバイスするとよいでしょう。第一のグラフから
- 工場数は圧倒的に中小工場が多い。
- ほとんどの工場が中小工場である。
が出てくると良いのですが、
・工場数は中小工場の方が多い。
のように「どれだけ」の修飾節を書けない児童がいます。この修飾節を書けないと、理科でも国語でも困ります。修飾節や形容詞を適切に書くことに対して児童がインセンティブを感じられるようになれるとよいですね。机間巡視のときに、的確な修飾節や形容詞、接続詞等を書いた児童のノートの該当箇所に赤丸をつけて「かっこいいね!」などとほめ、「〇〇さんは「主に」「圧倒的に」という言葉を使ったよ、かっこいいね」などのようにして語彙を共有する授業を心がけるとよいでしょう。表現に困ったときにぴったりとあてはまる語彙を学んだとき、語彙はもっともよく身に付くからです。
こうして、皆が特徴を挙げたことで、
- 工場数は圧倒的に中小工場が多い。
- 働く人の数は中小工場の方が多いが、その割合は全体の2/3程度である。
- 生産額は大工場の方がやや多いが、中小工場と同じくらいである。
- 機械工業では、大工場の生産額の方が多い。
- 重工業では大工場の生産額の方が多い。
- 軽工業では中小工場の生産額の方が多い。
などが並びました。ここで、156ページの下の左側の帯グラフは中小企業と大企業の「割合」に関するグラフであるのに対し、右側の帯グラフは「生産額」という絶対量に関する帯グラフである、ということを認識していた生徒が少なかったのがやや気になりました。本来ならば「重工業では、大工場の生産額の方が多い」と書くべきところ、「重工業では大工場の方が多い」と書いた児童が相当数いました。この2つは異義です。同義文判定が重要になるのは、このような場面においてです。ここは一歩踏み込んで、同義か異義かを確認するとさらに良かったでしょう。
ところで、2つめのグラフのラベルは「各工業の生産額にしめる中小工場と大工場の割合」です。「しめる」という言葉になじみのない児童は少なくありません。学習必須用語ですから、さらっと流さずに確認しておきたい語彙です。
ここまでで、今日のめあての半分である1が終わりました。「まだ2つめのめあてが終わっていないね」と山田先生は児童に確認させます。児童が時計に目をやり、「残り時間で2を頑張らないと」と思う様子がほほえましかったです。今日すべきことのどこまでが終わったか、とプログレスを意識する、ということは自学自習をスムーズに進めていく上でも必要になる能力です。授業時間の管理を先生が一方的にするのではなく、児童も意識することで、時間管理の方法を具体的な成功例や失敗例を体験することで学んでいくことができます。
さて、2つめは「 中小工場の特色や役割を読み取る」です。
見開き2ページの右側にそのことが書いてあります。「157ページの本文をよく読んで『中小工場の特色や役割』について書いてある部分に線を引こう。その上で、できるだけノートに箇条書きにしよう」と児童を励まします。ここは、中小工場の特色や役割が、3つの長い複文の中に埋め込まれています。その中から、児童は次のような特色を挙げました。
- 中小工場は、情報を交かんし、協力して製品の開発に取り組んでいる。
- 中小工場は、高い技術をもっている。
- 中小工場は、大工場の生産を支えている。
興味深かったのは「それぞれの中小工場でもっている高い技術を生かしてつくり出される製品は、大工場の生産を支えるとともに、わたしたちのくいらしの様々な場面で使われています。」の文から「中小工場は何をもっていますか?」に答えられる児童が大変少なかったことです。係り受け解析の能力が問われる場面です。
5年生にとって「もっている」というのは、「品物を所有していること」であって、「高い技術をもっている」ということが腑に落ちないのかもしれません。「もつ」という基本語彙であってもその使い方が高学年になると変化することで、児童がつまずくということをよく把握した上で課された箇条書き課題でした。
その上で、山田先生は157ページの写真と地図に着目させました。円筒の金属から複雑な形状の部品を作っている写真です。
「これは、中小工場で生産された製品ですが、それは、今出た3つの特色のうちのどれを表した写真ですか?」
という問いかけに対して、
- 高い技術を示した写真
という答えが多くの児童から聞かれました。手を挙げるか迷っていた下位の生徒も「ああ」という声が聞かれ、「高い技術をもつ」ということの具体イメージが持てたのではないかと思います。
次に、(やや駆け足になりましたが)157ページ右上の地図、「工場が多く集まる地域」に着目させました。まず、既習知識の確認です。
「どんなところに工場は集まっているかな」
「関東と関西」という答えもありましたが、先生が、おなかの周りをジェスチャーで示したことで「太平洋ベルト」という答えが引き出されました。その上で、さらに「どうしてここに工場が集まっているんだろう。今挙げた特徴から考えてみよう」と高度な問いかけをしました。
このような高度な問いは、特徴をあげずに問いかけると、答えが発散してしまい、どの意見が正しく、どの意見は間違っているのか、わからないまま授業が終わってしまいがちな部分です。この授業では、前もって特徴を挙げていたからこそ、
- 協力して製品をつくるのに都合がよいから。
- 大工場のそばに中小工場が集まるから。
など、論理的に推論をすることができました。
最後に、まとめを書いた後、各自がふりかえりを書きました。その中に、
「今日は中小工場の数や特色のことがよくわかった。次は大工場の特色について勉強したい」という意見がありました。
ところが、教科書は中小工場に多くのページ数を割いているのに、大工場については記述がないのです。
参観された文部科学省の塩見みづ枝審議官(初等中等教育局担当)は、「それは大変申し訳なかった」と苦笑しながら、「児童がこれだけ意欲をもって学んでいるので、興味関心に応える学習指導要領にしなくては」「教科書を『使い倒す』ことで、これだけ豊かな授業が生まれることに感銘を受けた」との感想を述べられました。
RSの概念に基づきつつ、しかも本来の科目の目標をしっかりと達成できた、まさに「読み解く力を育成する授業」でした。
全国どこの学校でも実践できる極めて質のよい授業を考案してくださった山田先生と板橋第二小学校に心から感謝します。
ワンポイントアドバイス
小学校の授業は、通常見開き2ページで一回の授業を組み立てます。社会科では、2つまたは3つの項目で2ページが構成されています。そこで、社会科のめあてをつくるとき、各項目をまとめた複文で全体のめあてを作ると、授業をスムーズに進めやすくなり、時間切れによる取りこぼしがなくなります。
山田先生のめあても、156ページで1つ、157ページで1つという2つのめあてで、授業全体のめあてが構成されていることがわかりますね。
考えてみよう
一人一台パソコンが小中学校に導入されつつあります。学校には、教科書を紙のままにするかデジタルにするか、迷っているところもあるでしょう。デジタル教科書は、キーワードで検索ができたり、知らない言葉に辞書が連動しているなどのメリットがあります。一方で、デジタル教科書が想定しているキーワード検索をして適切な箇所を参照したり、辞書機能を自ら使いこなすことは、高学年であっても困難であることが上記授業録からもわかります。
国立情報学研究所等の研究グループや教育のための科学研究所が行ったこれまでの研究成果から、以下のようなことがわかっています。
- 県立偏差値上位の高校であっても、デジタル化した教科書を自由に検索をして記述式問題(日本史)に答えるタスクの正答率が極めて低かった。一方、ほとんどの生徒が、「答えが書いてあるページ」は検索によって表示していた。つまり、検索の技巧が低いというより、検索して目的のページを表示しても、そこを読み解く力がないため、タスクに失敗したと考えられる。
- A町の小中学校において、RSTをふりがななしと総ルビをつけた状態半々で実施し、正答率を比較した。その結果、全学年で、ルビあり・なしで正答率は統計的に有意な差がなかった。加えて、小学6年生から中学2年生までは、ルビを活用していないと思われる(問題文を読む時間が有意に伸びていない)一方、中学3年生は問題文を読む時間が有意に伸びたので、ルビを活用したと考えられる。ただし、その中学3年生も正答率は上がっていない(むしろ下がった)。
デジタル教科書には、紙と異なり、様々な「押すことによって状態が変わるボタン」(リンクやルビ等)があります。小学生では授業中に集中が切れると、こうしたボタンを次々に押してしまい、元に戻ってこられなくなるという現象がよく見られます。
紙とデジタルを選ぶ上で参考になれば幸いです。
沖縄県立球陽中学校で研究授業をしました。
まだ最高気温が30度になる沖縄で、研究授業を実施しました。
今回、お招きいただいたのは沖縄県立球陽中学校です。中高一貫の公立学校です。迎えてくれたのは中学3年生の生徒のみなさん。礼儀正しく明るい笑顔が印象的な学校です。
授業のテーマは「偽定理を探せ!」
これは中学1年生から大学生までどの学年でも実践していただける授業として、『AIに負けない子どもを育てる』(新井紀子著、東洋経済新報社、2019年)でも紹介しています。冒頭で、「真偽が決まる文を命題という」という定義を紹介し、どのような文が命題で、どのようなものはそうでないかを区別できるようにします。その上で、真であることが証明された命題を「定理」と呼ぶと説明し、「今日、皆さんは数学者になって、命題の真偽を見分け、真だと思うものには証明をつけましょう。偽だと思うものには、偽である証拠を見つけましょう」と活動の概要を説明しました。
ここまで約5分ですが、すでに球陽中が、私が今まで「偽定理を探せ!」を指導した中で、ずば抜けて「よく耕されたクラス」であることを感じました。
よく耕されたクラスの特徴は、「集中できる」「聞ける」「待てる」にまず現れます。「どれが定理かどうかなんて、自分には関係ない」と思えば急速に興味を失うものです。経験が限られている児童生徒は、どうしても視野が狭い面があります。「待てない」「聞けない」ことで、可能性を狭め、世界への窓を閉じてしまうのを見ると残念に思います。
このクラスは、5分間、一人も脱落せずに話を聞いているので、今日はだいぶ先に連れて行ってあげられるな、と直感しました。
最初の問題は定番の「0は偶数か」問題です。
| 0は偶数である。 |
偶数に手を挙げた生徒が圧倒的多数でした。(※RSTで大学生や一般社会人の3人に2にが「0は偶数ではない」を選ぶのに比べて、球陽中の3年生がいかに定義を正確に読めるか、がわかります。)ただ、数名「これは偽定理」だと言いました。
意見が割れたときには、定義に戻ることが重要です。
偶数の定義は?というと手を挙げて次のように答えてくれた生徒がいました。
| 2で割り切れる整数を偶数という。 |
「0 割る」と聞くと、「できない」と反応するRST受検者は少なくありません。「どんな数も0では割れない」ということと混同しているのでしょう。0は2で割り切れます。やってみましょう。
0÷2=0 あまり 0
つまり、これは真の命題で、しかも証明がつきましたから、「定理」になりました。
ここで、「偶数を他の文章で定義できますか?」と聞きました。すると、
「整数の並びは偶数、奇数、偶数、奇数、・・・と順番に繰り返す」という意見が出ました。
「でも、整数の並びは、奇数、偶数、奇数、偶数、・・・と順番に繰り返しているともいえるのではありませんか?」と問いかけると、はっとして、「ああ、確かにそうです。これではだめです」と返事がありました。このように指摘をされたときに、自分で「はっ」とする、ことが学びではとても重要です。はっとして、ああそれではだめだと思うから自分で修正ができるのですから。「はっ」とする瞬間、子どもは一番自分ごととして学ぶと感じます。
そうこうしているうちに「2の倍数を偶数といいます」という意見が出ました。私が「変数を使ってみませんか?」と誘うと、「$$2n$$で表される整数。(ただし、$$n$$は整数)」という意見も出ました。定義は何種類か持っていると使い勝手が良いのです。それはおいおいわかってきます。
次も定番問題です。
| どんな素数も奇数である。 |
まず、素数の定義から振り返りました。
| 1とそれ自身以外は約数をもたない、1より大きい整数を素数という。 |
素数の定義は数学でしかありえないような複雑な形をしています。悪文といってもいいでしょう。けれども、それ以外表現のしようがないのです。平易な文では表現できないことが科学の中にはたくさんあります。
球陽中ではあっという間に、これは「偽定理」だと見抜かれました。理由は「2は偶数で素数だから」です。「反例」です。反例をみつければ、偽定理だということを簡単に説得できます。
次に挑んだのは次の命題です。
| 連続する2つの整数の和は、奇数になる。 |
こういうシンプルな命題を証明するにはコツがあります。それは式にすることです。式の中には「ことば」を含めることはできません。「連続する2つの整数の和」を式にするにはどうしたらよいだろう。
そう、変数を使えばいいんです。
|
連続する2つの整数の和は、$$n$$を整数として、$$n+(n+1)$$と表すことができる。 $$n+(n+1)=2n+1$$ なので、これは奇数である。 |
式にすることの良さは「式にすれば勝手に式が考えてくれるところ」(by ライプニッツ)にあります。変形すると、「奇数だ」という証拠が出てくるわけです。先ほど、偶数の定義として、「$$2n$$(ただし$$n$$は整数)と表せる数」という確認をしておいたことが、ここで効いてきます。
このクラスならば大丈夫と思い、最後はちょっと難しい問題を出しました。
| 連続する2つの整数の積は偶数になる。 |
一般に、いくつかの数に、ひとつでも偶数が混じっていれば、その積は偶数になります。
多くの生徒が「$$n(n+1)=n^2+n$$」という式を前に「うーん」と悩んでいます。その悩める時間の長さこそが、生徒の伸びしろになります。
ここには答えは書きません。みなさんもぜひ「うーん」と悩んでみてください。
板橋区学びのエリア「板橋のiカリキュラム開発重点校」研究授業が実施されました。
10月1日、令和2年度板橋区学びのエリア「板橋のiカリキュラム開発重点校」研究授業(第2回目)が、板橋第一中学校で行われました。教育のための科学研究所からは、新井紀子代表のほか、菅原真悟上席研究員、犬塚美輪学芸大学准教授(教育のための科学研究所客員研究員)が参加し、各科目の研究授業の参観、助言を行いました。
研究授業のひとつである中学2年生の数学は、一次関数が題材でした。関数は中学生にとって最も理解が難しい内容のひとつで、一次式と一次関数の区別がつかない生徒も少なくありません。教育指導要領が求める「数学を使うことの良さ」を実感させることもなかなか難しい単元です。
本授業では、教育のための科学研究所からの事前助言に基づき、3つの問いから始まりました。
次の文章のうち、「変化する2つの量」の関係が「一次関数」になっているものはどれかを考える問いです。
- ダイエットに挑戦したが、体重が増えた日もあれば減った日もあった。
- ひまわりの種をまいたところ、芽が出てからしばらくはなかなか成長しなかったが、その後ぐんぐん成長し、花が咲くころに成長が止まった。
- 冷たいペットボトル飲料をある保冷バックに入れて持ち歩いたところ、その飲料は時間がたつにつれてほぼ一定の割合で温度が上がることがわかった。
クラス全員が3が一次関数であると手を挙げました。
授業者はここで流すことなく、(1)なぜ3は一次関数だと思ったのか、(2)1と2はなぜ一次関数ではないと思ったのか、を生徒から文章で引き出していました。これは、具体例同定(理数)の活動として位置づけられました。
「3は時間に対して一定の割合で温度が上がるので一次関数になる」「1は時間に対して体重が一定の割合で増えても減ってもいないので一次関数ではない」「2は時間に対してひまわりの成長が一定でないから一次関数ではない」
ただし、2について「変化する2つの量」が何かがわからない生徒もいました。「ひまわりの高さ」が明示的に文中に書いてないので迷うようです。このように、ふつうに書かれている文章の中で、着目すべき数量が何かを取り出すこと、そして、その関係を式で表すことの良さ(=未来や過去を予測できる)を感じてほしいと思います。
次に授業者はプリントを配布しました。そこには、実際にペットボトル飲料の温度がどのように変化したかが表になっています。
| 分 | 20 | 30 | 40 | 50 | 60 |
| ℃ | 5.2 | 5.8 | 6.4 | 6.9 | 7.6 |
まず、「変化量」を見ます。小数が入る2桁の引き算を4回しなければならないのですが、結構時間がかかりました。やはり小学校で3桁の計算までは苦労なくできるようになって中学校に進学しておくと、中学校の授業では概念理解に集中できますね。適度な量のドリル、そして中学入学後も一定量の四則演算ドリルは必要だということがわかります。
さて、差分は、0.6, 0.6, 0.5, 0.7になりました。平均すると「10分ごとに約0.6度上がる」と言えるというところまでは全員が納得できました。ところが、「1分(1単位)ごとにどれだけ変化するか」がなかなかわかりません。
「10分で0.6度上がる」⇔「1分で0.06度上がる」
の変換が難しいようです。これはRSTでは「同義文判定」に位置付けられる内容です。
このあと、表をグラフで表し、式にしていきます。その際、教科書に書かれている一次関数の定義を振り返ります。
|
一次関数とは$$y$$を$$x$$の一次式で表せる関数のことである。 $$ y=ax+b $$ $$a,b$$は定数 |
この定義を正確に理解するのが極めて難しいことが、RSTのこれまでの結果からわかっています。
まず、$$a,b$$は定数という但し書きを読まずに、前提なしに「$$ax+b $$」という形の式は一次式だと勘違いする生徒(学生)は東大生にも少なくありません。また、「$$y$$を$$x$$の1次式で表せる関数」を正しく読解できる生徒は少なく、その後に書いてある$$ y=ax+b $$を一次式だとほとんどの生徒が読みます。正しくは、$$a,b$$は定数のとき$$ax+b $$は一次式であり、そのような$$x$$の一次式として$$y$$を表せる、つまり$$ y=ax+b $$と表現できるとき、一次関数といいます。
このように解像度高く読まないと、数学では様々な概念を混同してしまいますので、注意が必要です。授業者には、生徒の興味関心を引くだけでなく、解像度高い読解を促すような問いかけも意識してほしいところです。
プリントで示された表には初期値、つまり最初の温度が書かれていません。20分後からの表だけです。$$x=20$$と$$x=60$$の$$y$$の値から、連立方程式で式を求めるか、変化の平均値が1分ごとに0.06度であることから$$ a=0.06 $$は得られているとし、20分後の値から一次方程式を解くことで、切片である$$b$$を求めるなど、いくつかの方法で生徒たちは、求めるべき式、
$$y=0.06x+4$$
を導出しました。一人ひとりだとなかなか難しかったので、隣どうしで話し合いを行うことで計算間違いを見つける等の手がかりを得て、式にたどり着けた生徒が多かったようです。ここでも小数のある計算、特に割り算に中学2年の段階でも課題が残っていることがわかりました。
こうして、「ペットボトルの中の飲料は、時間を$$x$$としたとき、温度yは$$ y=0.06x+4 $$という式に従って上昇する」というまとめで授業は終わりました。
ここで、新井が手を挙げて、こんな問いかけをしました。
| では、1600分後には、ペットボトル飲料は沸騰しますか? |
これは生徒も想定外だったようでざわつき、「そんなことにならない」と言いましたが、「だとしたら、それは特定の$$x$$の範囲においてのみ一次関数である」ということに気づいた生徒もいたようです。次回の展開が楽しみです。
※冒頭の「ひまわりの成長」についての文章はもう少し詳しく書いたものを、2011年に実施された日本数学会第一回大学生基本調査のプレ調査として2010年に行われた調査で「ひまわりの成長を適切に横軸と縦軸をとって、概形を表しなさい」という問題として出題しました。教員養成系大学で大変悲惨な結果になったことが思い出されます。










 リーディングスキルテストとは何か?
リーディングスキルテストとは何か? リーディングスキルテストの申込方法について
リーディングスキルテストの申込方法について
 受検人数を入力するとおおよその受検料が表示されます
受検人数を入力するとおおよその受検料が表示されます






